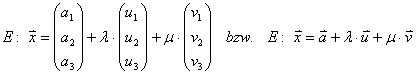
Hessenormalform der Ebene (Nur R³)

Die Normalengleichung der Ebene

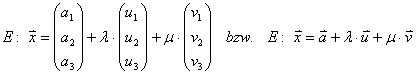
Das ist die Parameterform der Ebenengleichung.

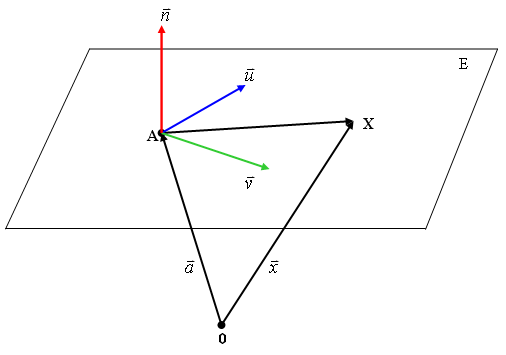
Man multipliziert die Ebenengleichung mit einem beliebigen Normalenvektor

Die ist die NORMALENGLEICHUNG der Ebene.

Nun schreibt man sie etwas anders und multiplizieren sie aus, dadurch erhält man die KOORDINATENFORM.

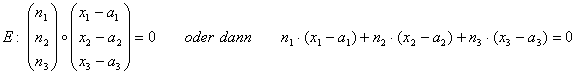
Beispiel:

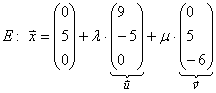
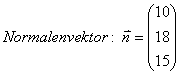
• Man testet kurz ob der Normalenvektor auch zu den beiden Richtungsvektoren senkrecht ist.

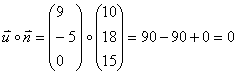
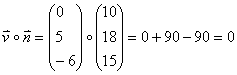
• Dann kann man die Normalengleichung angeben.

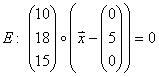
• Daraus ermittelt man die Koordinatenform.

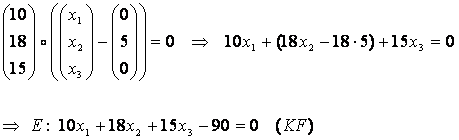
An diesem Beispiel sieht man, dass sich der Normalenvektor aus den Koeffizienten der Koordinatenform ergibt!

Dieser Umstand ermöglicht uns einfache Umformungsschemen!

Parameterform zu Koordinatenform
 

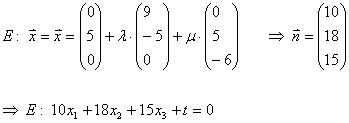
Man erhält also mittels des Normalenvektors schnell die Koordinatenform, aber nun fehlt noch t:

Um t zu erhalten setzt man einfach den Aufpunkt der Ebene in die KF ein!

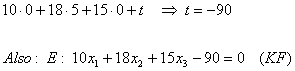
Koordinatenform zu Parameterform
 

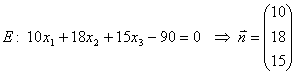
Um zur Parameterform zu kommen benötigen wir aber zwei Richtungsvektoren!

• Man kann zum Beispiel die dreifache Punktprobe anwenden! D.h. man sucht sich nacheinander drei Punkte, die die KF erfüllen!

z.B. A=(9,0,0)    ;B=(0,5,0)    ;C=(0,0,6)

• somit hat man also AB und AC als Richtungsvektoren
  (Mit der dreifachen Punktprobe kann man auch überprüfen ob die Koordinatenform mit der Parameterform übereinstimmt!)

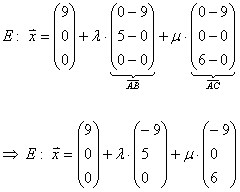
Oder man löst die Koordinatenform zuerst nach einer Variable auf.

• Dann überlegt man sich vorteilhafte Koeffizienten und Parameter für die übrigen Variablen!

• Man wirft dies nun alles in einen Pot und "zieht ihn dann auseinander" und zwar so dass die einzelnen Parameter übereinander stehen.

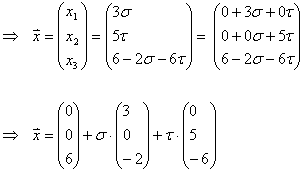
Beispiel 1:    Wandle die Parameterform der Ebene in die Koordinatenform um.

>> Lösung >>

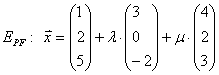
Beispiel 2:    Bilde aus der Koordinatenform die Parameterform.

>> Lösung >>